Quantum Computing, Principle 1: Superposition
- rinaismailati
- Dec 18, 2020
- 4 min read
Updated: Aug 16, 2021
Superposition is one of the two pillars of quantum computers. Let's have a closer look at this phenomenon.
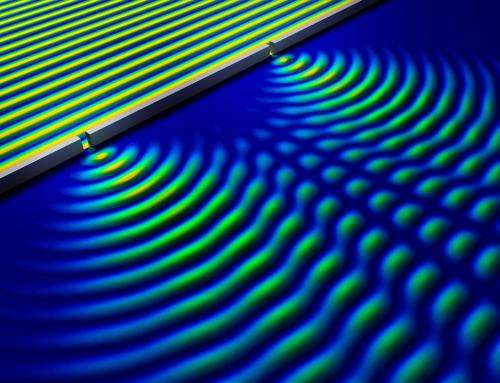
Superposition of water waves
Consider throwing two stones in a pond of water at the same time. Each of them will cause ripples on the surface of the water or circles that start spreading out from the source (the stone). If the stones are located close enough to each other, the circles generated by each of them will interfere with each other, as shown in the figure below. On the interference region, we see peaks and valleys. We observe constructive and destructive interference. The interference pattern depends on the amplitude, frequency, and phase of the waves coming from the two sources. Here you can play with an interference simulator by changing the number of sources, wavelength and determine whether the two waves are in phase or out of phase. When the two sources are in phase (the difference between the respective phases is 0), they emit peaks and valleys at the same time. When the two sources are out of phase (there difference between the respective phases is pi radians), while one of the sources emits a peak, the other one emits a valley. When the waves from the two sources interfere with each other, in some points valleys will meet valleys and peaks will meet peaks, thus leading to constructive interference. There where peaks and valleys overlap, we have destructive interference. Here we are dealing with motionless or standing waves. In this simplified explanation, we are always assuming that the frequency of the two waves is the same.

The double-slit experiment
The double-slit experiment shows that light and matter behave both as waves and particles. First, it was the idea of Thomas Young to use a coherent light to hit a barrier with two slits. Through this experiment he wanted to show the wavelike nature of light. After light hits the two slits, they will serve as two sources and the interference pattern will appear, as we saw earlier in the example of water waves. The fringes on the screen show the constructive and destructive interference of the wavelets. 100 hundred years later, G. I. Taylor used a similar setup to show the corpuscular nature of light, using single photons to hit the barrier. After hitting the barrier with many photons, he expected to see on the screen only two shinning points behind each slit, because he reasoned that if a photon is a particle it will pass through one of the slits and hit the screen just behind the slit. What he saw in fact was a different result! He saw the same fringes that Young had seen when he wanted to prove the wavelike nature of light! Wait a minute. Do these fringes appear even when only one photon hits the slits? They do! The photon passes through both the slits, just like a wave, and then the interference patterns occur behind the slits, as in the case of the experiment of Young. This experiment showed the wave nature of light. Since light is both a particle and a wave, we refer to this concept as the wave-particle duality.

Left: Young's original experiment, using coherent light. Right: Taylor's experiment, using one photon at a time. (Source)
Another important result that the double-slit experiment showed, was the superposition principle, that particles can exist in multiple states and simultaneously in multiple positions. In order for the interference to happen (and the fringes to appear), the particle must travel through both slits at the same time. If we place a detector just behind a slit, the fringes will disappear and we will only see two lines on the screen, as we would expect if a particle was passing through the slits.
Superposition and quantum computers
How do quantum computers take advantage of superposition?
In quantum physics, particles are described by the wavefunction. Its solutions, indicated by the Greek letter ψ, express the probability amplitude of a particle being in a particular position or state. Suppose we flip a fair coin with 50% probability of landing head and 50% probability of landing tail. The state that we measure can be expressed as:
where α and β are numbers ranging from 0 to 1. Their squared values give the probability of measuring the state |0〉or the |1〉respectively. The notation |〉is called a ket and it is a vector. For example the zero state |0〉is the vector (0 1) whereas the one state |0〉is the vector (1 0). In our coin example you can imagine the state zero representing the head, and the state one representing the tail (arbitrary choice). In the case of a fair coin both the squares of α and β are equal to 0.5. If the coin was biased and the head result was favored, α squared would have a value bigger than 0.5, for example, 0.7, showing that on average, in 100 flips, the coin would land 70 times head.
A classical system can be in one of the states only at a given time. On the contrary, quantum systems can be in both states simultaneously. In our previous article, we saw the example of the electron with its spins "up" and "down". The spin of an electron can be simultaneously in both states until the moment that we measure it (wave function collapse). When we measure the spin direction, we will measure either the state "up", or the state "down". The probabilities for measuring each of these states are determined by the coefficients α and β in the wavefunction. The two states that are part of the superposition are called basis states. One qubit has two basis states (e.g. the two spin orientations of an electron, or two energetic levels in an atom). For n qubits, there are 2^n states. With three qubits there are 2^3 = 8 possible states. If we have n classical bits, one state occurs on only of the 2^n possibilities, whereas for n qubits, all 2^n possibilities can exist at the same time.
Many quantum algorithms have been designed to use the superposition principle, thus performing tasks exponentially faster than classical computers.
コメント